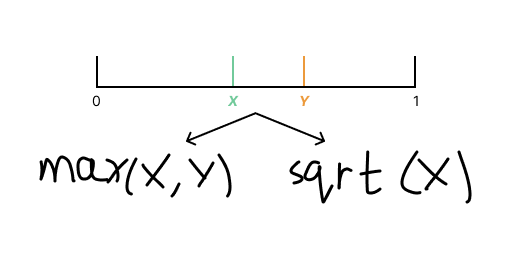
max(X, Y) or sqrt(X)?

Intro

I originally learnt this from Stand-up Maths who creates excellent entertaining videos about fun results like this one. Suppose you have a random number generator that returns numbers between 0 and 1 with equal probability. Would you rather pick the maximum of two random numbers or the (positive) square root of one random number if you want the largest value?

In more formal mathematical terms, let $X$ and $Y$ be two independent random variables with the standard uniform distribution.

$X, Y \sim U(0, 1)$

How do the distributions of $max(X, Y)$ and $sqrt(X)$ relate to each other?

First observations

What do $max(X, Y)$ and $sqrt(X)$ do at a basic level? Imagine $X$ as a random point on a line between 0 and 1.

Given a particular value of $X$, $max(X, Y)$ must be greater than or equal to $X$ by definition.

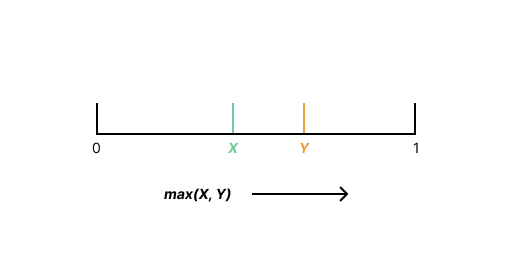
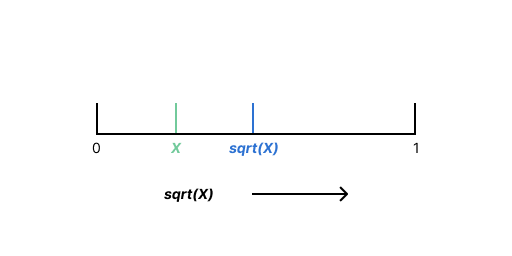
Similarly, defining $sqrt(X)$ as the unique positive square root must be greater than or equal to $X$ due to the value of $X$ being in the interval $[0, 1]$. For example, $\sqrt{0.25}=0.5$, $\sqrt{0.5} \approx 0.707$.

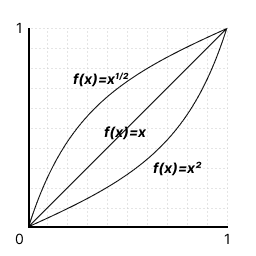
As well as being monotonic (increasing) functions, both $f(x) = x^2$ and $f(x) = sqrt(x) = x^{1/2}$ are in fact continuous, bijective functions on the interval $[0, 1]$. This means given any value $y \in [0, 1]$, there exists a unique value $x \in [0, 1]$ such that $f(x) = y$.

Probability distribution

What's the probability that $max(X, Y)$ is less than or equal to a given value $α \in [0, 1]$?

Recall that $X$ and $Y$ are random variables with the standard uniform distribution so their cumulative distribution function is simply the width of the interval within $[0, 1]$:

We also know that $X$ and $Y$ are independent so:

What's the probability that $sqrt(X)$ is less than or equal to a given value $α \in [0, 1]$?

From our first observations we noticed that squaring is a monotonic increasing function on $[0, 1]$ which means that it preserves an inequality when applied to both sides.

Their cumulative distribution functions are equal everywhere and therefore $max(X, Y)$ and $sqrt(X)$ are identically distributed!

Transforming the problem

We can transform the problem to view the intuition behind this visually. As we have two random independent variables, rather than a random point on a 1D line imagine $X$ and $Y$ as a random point on a 2D grid where each point is equally likely to be picked.

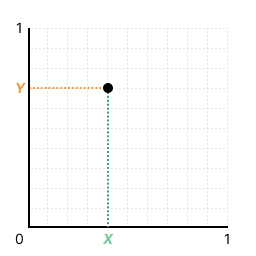
In this 2D grid, we see that the boundary lines $X = α$ and $Y = α$ define a square such that any point inside this square satisfies $max(X, Y) \leq α$.

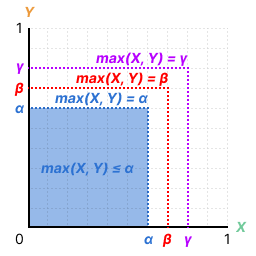
As each point is equally likely to be picked, the probability of picking a point inside the square is proportional to the area of the grid and we get the same result:

For $sqrt(X)$, we extend the 1D line to a 2D grid where each value $sqrt(X) = α$ defines a unique square $X$ in the 2D grid where the value of $X$ is the area of the square $X = α^2$ and vice versa.

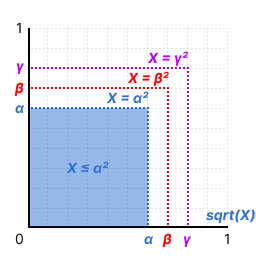
From this we can visually see the same inequality as before:

Conclusion

The result is hard to believe at first. How could $max(X, Y)$ and $sqrt(X)$ possibly be identically distributed? With this magic setup these two random functions can in fact be linked together where introducing the second independent identically distributed random variable $Y$ to $X$ has an effect of introducing "squaring" to the problem.

We also saw that transforming the problem to visualise the problem in a new way can help provide intuition into how a structure behaves and aid constructing a proof. This powerful technique pops up often in mathematics and can remarkably link one problem to another, sometimes in a completely different branch of mathematics!