Ramsey Theory - The Party Problem

Intro

How many people must be at a party to guarantee that at least $m$ people all know each other or at least $n$ people all do not know each other? This is the Party Problem and is a fun result from the area of mathematics known as Ramsey Theory.

Triangles with two colours

Consider the case $m, n = 3$. We'll sketch a proof that the minimum required number of people to guarantee at least three people will all know each other or all do not know each other is six.

Transforming this problem to a graph we start with the complete graph $K_i$ with $i$ nodes and all possible edges between them. Each node represents a person at the party and we colour the edges either red or blue with red representing the two people at either end of the edge know each other and blue representing the two people at either end of the edge do not know each other. A clique of a graph $G$ is defined as a subgraph of $G$ that is also complete i.e. has all possible edges between its nodes. We are therefore looking for a red or a blue clique of size three ($K_3$), or in other words a red or a blue triangle.

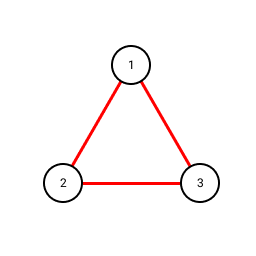Red triangle represents all three people know each other

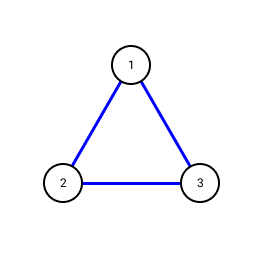Blue triangle represents all three people do not know each other

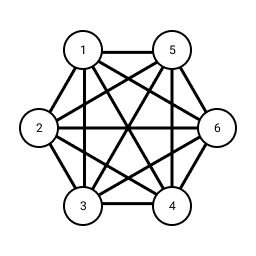
First, we show a counterexample that the party must have more than five people. Here is a red/blue colouring of $K_5$ which does not contain a red or blue triangle:

$K_5$ counterexample

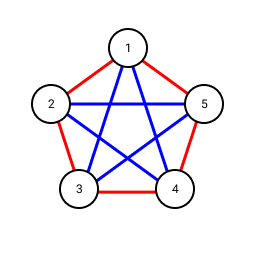
Now we must show that for any red/blue colouring of $K_6$ there must always be a red triangle or a blue triangle. Consider a node of $K_6$ and the colours of its five edges to the other five nodes in the graph:

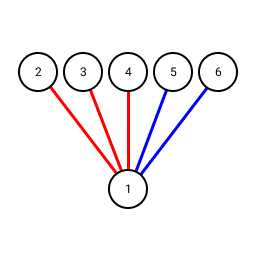A node and its edge colours in $K_6$

By the pigeonhole principle there must be at least three edges with the same colour. Without loss of generality let us assume we are looking at node 1 and the edges to 2, 3 and 4 are red. If this is not the case we can relabel the nodes and reverse the role of red and blue to make this true. Now, consider the colours of the edges between nodes 2, 3 and 4:

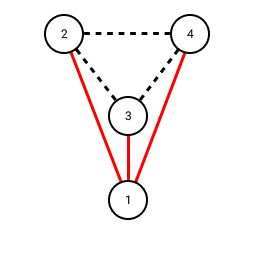Edges between 2, 3 and 4

We have two cases:

• If there is at least one red edge we complete a red triangle
• If there are no red edges then they must all be blue and we have a blue triangle

Therefore, the minimum number of people at a party to guarantee at least three people will all know each other or all do not know each other is six!

Ramsey's Theorem

More generally, Ramsey's Theorem states that for any positive integers $m, n$ there exists a minimum number $R(m, n)$ called a Ramsey number such that for any complete graph with $R(m, n)$ vertices will contain either a red clique of size $m$ or a blue clique of size $n$.

By the above, we've shown that $R(3, 3) = 6$.

You can find some other Ramsey numbers at Wolfram MathWorld for example for a larger party to guarantee at least four people will all know each other or all do not know each other you would need a minimum of $R(4, 4) = 18$ people.